Difference between revisions of "Graphviz"
m (1 версия) |
(Массовая правка: замена Category:Справка на <noinclude>Category:Справка</noinclude>) |
||
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
'''Graphviz''' — это разработанный специалистами лаборатории AT&T пакет утилит по автоматической визуализации графов, заданных в виде текстового описания. Пакет распространяется с открытыми исходными файлами и работает на всех операционных системах, включая Windows, Linux/Unix, Mac OS. Самой интересной программой пакета является «dot», автоматический визуализатор направленных графов, который принимает на вход текстовый файл со структурой графа, а на выходе формирует граф в виде графического, векторного или текстового файла. | '''Graphviz''' — это разработанный специалистами лаборатории AT&T пакет утилит по автоматической визуализации графов, заданных в виде текстового описания. Пакет распространяется с открытыми исходными файлами и работает на всех операционных системах, включая Windows, Linux/Unix, Mac OS. Самой интересной программой пакета является «dot», автоматический визуализатор направленных графов, который принимает на вход текстовый файл со структурой графа, а на выходе формирует граф в виде графического, векторного или текстового файла. | ||
| − | |||
| − | |||
| − | + | == Быстрый старт == | |
| + | Входной файл для программы «DOT» является обычным текстовым файлом на специальном языке разметки графа. Структура файла очень простая, например, | ||
| + | <nowiki><graph> | ||
digraph G{ | digraph G{ | ||
Рождение->Юность->Зрелость->Старость->Смерть; | Рождение->Юность->Зрелость->Старость->Смерть; | ||
| Line 10: | Line 10: | ||
Зрелость->Смерть; | Зрелость->Смерть; | ||
} | } | ||
| − | + | </graph></nowiki> | |
на выходе будет | на выходе будет | ||
<graph> | <graph> | ||
| − | + | digraph G{ | |
| − | + | graph[fontname="Segoe UI"]; | |
| − | + | Рождение->Юность->Зрелость->Старость->Смерть; | |
| − | + | Юность->Смерть; | |
| − | + | Зрелость->Смерть; | |
| + | } | ||
</graph> | </graph> | ||
| Line 43: | Line 44: | ||
Поздравляем! Теперь вы способны рисовать графы в [[{{SITENAME}}]]. Остальной текст будет посвящен некоторым тонкостям использования [[Graphviz]]. | Поздравляем! Теперь вы способны рисовать графы в [[{{SITENAME}}]]. Остальной текст будет посвящен некоторым тонкостям использования [[Graphviz]]. | ||
| − | = Внешний вид графа = | + | == Внешний вид графа == |
«Dot» позволяет изменять внешний вид графа. Например, можно изменять форму фигур (прямоугольники, овалы, круги, параллелограммы, многоугольники), цвет и шрифт текста, цвет фона фигур, стиль стрелок и рамок фигур, подписи стрелок и т. д. | «Dot» позволяет изменять внешний вид графа. Например, можно изменять форму фигур (прямоугольники, овалы, круги, параллелограммы, многоугольники), цвет и шрифт текста, цвет фона фигур, стиль стрелок и рамок фигур, подписи стрелок и т. д. | ||
Итак, основные объектами являются узлы («node») и ребра («edge»). Для того, чтобы настроить свойства всех узлов или ребер нужно вначале использовать команды | Итак, основные объектами являются узлы («node») и ребра («edge»). Для того, чтобы настроить свойства всех узлов или ребер нужно вначале использовать команды | ||
| Line 83: | Line 84: | ||
Существенна только первая цифра. Число 6.7 подобрано эмпирически, оно обеспечивает печать полной картинки при настройках IE по умолчанию. | Существенна только первая цифра. Число 6.7 подобрано эмпирически, оно обеспечивает печать полной картинки при настройках IE по умолчанию. | ||
| − | = Уровни в графах = | + | == Уровни в графах == |
В «Dot» присутствует возможность связать узлы графа не только стрелками, но и уровнями отображения, что позволяет создавать шкалу и располагать узлы графа соответственно данной шкале. Для связывания используется следующая конструкция: | В «Dot» присутствует возможность связать узлы графа не только стрелками, но и уровнями отображения, что позволяет создавать шкалу и располагать узлы графа соответственно данной шкале. Для связывания используется следующая конструкция: | ||
| Line 125: | Line 126: | ||
</graph> | </graph> | ||
| − | = Многосекционный узлы = | + | == Многосекционный узлы == |
Dot позволяет создавать многосекционные узлы при это каждая секция может быть поименована, и тогда ребра можно продоводить между секциями и узлами. | Dot позволяет создавать многосекционные узлы при это каждая секция может быть поименована, и тогда ребра можно продоводить между секциями и узлами. | ||
| Line 156: | Line 157: | ||
</graph> | </graph> | ||
| − | = Гиперссылки на графах = | + | == Гиперссылки на графах == |
Можно использовать атрибут «URL», задавая относительные или абсолютные гиперссылки для узлов и ребер. Например | Можно использовать атрибут «URL», задавая относительные или абсолютные гиперссылки для узлов и ребер. Например | ||
| Line 191: | Line 192: | ||
</graph> | </graph> | ||
| − | = Кластеры в графах = | + | == Кластеры в графах == |
Программа «Dot» позволяет объединять узлы графов в кластеры для подчеркивания общности. | Программа «Dot» позволяет объединять узлы графов в кластеры для подчеркивания общности. | ||
| Line 252: | Line 253: | ||
</graph> | </graph> | ||
| − | = Цвета и черно-белая печать= | + | === Цвета === |
| + | Graphviz позволяет использовать широкую цветовую палитру, | ||
| + | задавая цвета или по именам, в одной из известных палитр: | ||
| + | * [http://www.graphviz.org/content/color-names#x11 Палитра X11] | ||
| + | * [http://www.graphviz.org/content/color-names#svg SVG] | ||
| + | |||
| + | * [http://www.graphviz.org/content/color-names#brewer Набор палитр Brewer-а], что удобно при автоматической генерации схем — задаваемые числовым индексом цвета в более-менее вменяемой палитре. | ||
| + | |||
| + | Кроме именованных цветов, можно использовать обычное трехбайтное шестнадцатиричное кодирование | ||
| + | color="#FF0EDD" | ||
| + | и выбирать цвета из палитры, например, на http://www.colorpicker.com/ | ||
| + | |||
| + | ==== Цвета и черно-белая печать ==== | ||
| + | |||
Graphviz позволяет использовать широкую цветовую палитру, однако, стоит не забывать, что контрастно выглядящие на цветном мониторе цвета, могут быть совершенно неразличимы после черно-белой печати. После проделанных экспериментов ({{Bug|11015}}), можно рекомендовать следующие палитры цветов (иллюстрированы на цвете ребер графа): | Graphviz позволяет использовать широкую цветовую палитру, однако, стоит не забывать, что контрастно выглядящие на цветном мониторе цвета, могут быть совершенно неразличимы после черно-белой печати. После проделанных экспериментов ({{Bug|11015}}), можно рекомендовать следующие палитры цветов (иллюстрированы на цвете ребер графа): | ||
| Line 273: | Line 287: | ||
</graph-print> | </graph-print> | ||
| − | = Формы вершин = | + | == Формы вершин == |
Перечислим палитру возможных форм вершин (узлов). | Перечислим палитру возможных форм вершин (узлов). | ||
| Line 317: | Line 331: | ||
</neato> | </neato> | ||
| − | = Окончания ребер = | + | == Окончания ребер == |
Можно задавать стиль офомления начала («arrowtail») и конца («arrowhead») дуг (ребер): | Можно задавать стиль офомления начала («arrowtail») и конца («arrowhead») дуг (ребер): | ||
| + | |||
| + | {{Warning}} Чтобы работал arrowtail, для ребра нужно указать свойство '''dir=both''' или '''dir=back'''. | ||
<circo> | <circo> | ||
digraph G{ | digraph G{ | ||
| + | size="6.7,15"; | ||
edge [arrowtail="none"] | edge [arrowtail="none"] | ||
| Line 348: | Line 365: | ||
</circo> | </circo> | ||
| − | = Неориентированные графы = | + | == Неориентированные графы == |
Наряду с рисованием ориентированных графов, есть несколько методов для автоматического рисования неориентированных графов (будем рассматривать их на примере несложной ER-диаграммы). | Наряду с рисованием ориентированных графов, есть несколько методов для автоматического рисования неориентированных графов (будем рассматривать их на примере несложной ER-диаграммы). | ||
В отличие от автоматического рисования направленных («directed») графов, основанных на ранговой модели, есть несколько подходов к раскладке ненаправленных графов. | В отличие от автоматического рисования направленных («directed») графов, основанных на ранговой модели, есть несколько подходов к раскладке ненаправленных графов. | ||
| − | == Graph == | + | === Graph === |
Ненаправленный граф можно нарисовать с помощью рангового подхода (несмотря на ненаправленность ребер) — будет использоваться программа «dot». Как это будет выглядеть для простой ER-диаграммы, можно увидеть ниже. | Ненаправленный граф можно нарисовать с помощью рангового подхода (несмотря на ненаправленность ребер) — будет использоваться программа «dot». Как это будет выглядеть для простой ER-диаграммы, можно увидеть ниже. | ||
<graph> | <graph> | ||
| Line 383: | Line 400: | ||
Очевидна неоптимальность такого подхода для неориентированных графов. | Очевидна неоптимальность такого подхода для неориентированных графов. | ||
| − | == Neato == | + | === Neato === |
Метод «neato» использует «энергетическую» (''spring'') модель, по сути, близкую к методу искуственного отжига — начиная с некоторого состояния вершины перемещаются, чтобы минимизировать некую потенциальную энергию. Рекомендуем для ненаправленных графов общего вида. | Метод «neato» использует «энергетическую» (''spring'') модель, по сути, близкую к методу искуственного отжига — начиная с некоторого состояния вершины перемещаются, чтобы минимизировать некую потенциальную энергию. Рекомендуем для ненаправленных графов общего вида. | ||
| Line 413: | Line 430: | ||
</neato> | </neato> | ||
| − | == FDP == | + | === FDP === |
Метод «fdp» по сути, близок к методу «neato», и использует другую разновидность «энергетического» («spring») подхода. Также рекомендуется для ненаправленных графов общего типа. | Метод «fdp» по сути, близок к методу «neato», и использует другую разновидность «энергетического» («spring») подхода. Также рекомендуется для ненаправленных графов общего типа. | ||
| Line 445: | Line 462: | ||
| − | == Twopi == | + | === Twopi === |
Метод «twopi» рисует графы с радиальной раскладкой. По сути одна вершина выбирается центральной, и помещается в центр, а остальные размещаются на последовательности концентрических орбит, вокруг этой вершины. Т.е. все вершины на расстоянии в «одно ребро» от центра, лежат на первой орбите, «в два ребра» — на второй и т. д. | Метод «twopi» рисует графы с радиальной раскладкой. По сути одна вершина выбирается центральной, и помещается в центр, а остальные размещаются на последовательности концентрических орбит, вокруг этой вершины. Т.е. все вершины на расстоянии в «одно ребро» от центра, лежат на первой орбите, «в два ребра» — на второй и т. д. | ||
| Line 476: | Line 493: | ||
</twopi> | </twopi> | ||
| − | == CIRCO == | + | === CIRCO === |
Метод «circo» использует «circular layout». Выделяются двусвязные компоненты (каждая вершина имеет по крайней мере два ребра) и вершины этих компонент рисуются на некотором круге. «Дополнительные» ребра рисуются радиально и далее процесс повторяется. Пересечение ребер внутри круга минимизируется максимально возможным выносом ребер с круга за его периметр. | Метод «circo» использует «circular layout». Выделяются двусвязные компоненты (каждая вершина имеет по крайней мере два ребра) и вершины этих компонент рисуются на некотором круге. «Дополнительные» ребра рисуются радиально и далее процесс повторяется. Пересечение ребер внутри круга минимизируется максимально возможным выносом ребер с круга за его периметр. | ||
| Line 506: | Line 523: | ||
</circo> | </circo> | ||
| − | = Версии для печати = | + | == Версии для печати == |
Как известно, трудно добиться хорошего результата одновременно на экране и на принтере, в силу разных разрешений. Картинка экранного разрешения будет плохо (с «зазубринами») выглядеть на принтере, а картинка печатного разрешения, будет очень плохо выглядеть на экране (к сожалению, современные броузеры выполняют очень примитивный ресайзинг картинок при показе), и будет достаточно много «весить». Все соображения о печатных картинках также относятся к случаю, когда вы переносите (например, копируя вебстраницу из броузера через клипборд) содержимое MediaWiki-статьи в MS Word или другой текстовый редактор. | Как известно, трудно добиться хорошего результата одновременно на экране и на принтере, в силу разных разрешений. Картинка экранного разрешения будет плохо (с «зазубринами») выглядеть на принтере, а картинка печатного разрешения, будет очень плохо выглядеть на экране (к сожалению, современные броузеры выполняют очень примитивный ресайзинг картинок при показе), и будет достаточно много «весить». Все соображения о печатных картинках также относятся к случаю, когда вы переносите (например, копируя вебстраницу из броузера через клипборд) содержимое MediaWiki-статьи в MS Word или другой текстовый редактор. | ||
Для такого, «печатного» случая (т. е. если у вас не примитивные графы, и вы собираетесь их печатать или переносить в другую систему верстки), мы сделали «печатную версию» всех перечисленных графов, с разрешением около 200 DPI. Для этого надо использовать те же самые тэги с постфиксом «-print», например «graph-print»,«neato-print», и т.п.: | Для такого, «печатного» случая (т. е. если у вас не примитивные графы, и вы собираетесь их печатать или переносить в другую систему верстки), мы сделали «печатную версию» всех перечисленных графов, с разрешением около 200 DPI. Для этого надо использовать те же самые тэги с постфиксом «-print», например «graph-print»,«neato-print», и т.п.: | ||
| Line 527: | Line 544: | ||
Желательно не использовать для совершенно тривиальных графов, или графов, которых вы не собираетесь печатать. | Желательно не использовать для совершенно тривиальных графов, или графов, которых вы не собираетесь печатать. | ||
| − | = Ссылки и дополнительная документация = | + | == Ссылки и дополнительная документация == |
Онлайн-документация, +последние изменения, FAQ и прочее можно найти на домашней странице пакета | Онлайн-документация, +последние изменения, FAQ и прочее можно найти на домашней странице пакета | ||
http://www.graphviz.org/Documentation.php | http://www.graphviz.org/Documentation.php | ||
| + | {{replicate-from-custiswiki-to-lib}} | ||
| − | + | <noinclude>[[Category:Справка]]</noinclude> | |
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
Latest revision as of 14:49, 1 September 2015
Graphviz — это разработанный специалистами лаборатории AT&T пакет утилит по автоматической визуализации графов, заданных в виде текстового описания. Пакет распространяется с открытыми исходными файлами и работает на всех операционных системах, включая Windows, Linux/Unix, Mac OS. Самой интересной программой пакета является «dot», автоматический визуализатор направленных графов, который принимает на вход текстовый файл со структурой графа, а на выходе формирует граф в виде графического, векторного или текстового файла.
Contents
Быстрый старт
Входной файл для программы «DOT» является обычным текстовым файлом на специальном языке разметки графа. Структура файла очень простая, например,
<graph>
digraph G{
Рождение->Юность->Зрелость->Старость->Смерть;
Юность->Смерть;
Зрелость->Смерть;
}
</graph>
на выходе будет
Программа «Dot» сама распознает все связи графа и упорядочит его таким образом, чтобы было наименьшее количество пересечений.
Чтобы использовать «dot»-графы в Wiki4Intranet, используйте следующий синтаксис:
<graph>
digraph G{
Рождение->Юность->Зрелость->Старость->Смерть;
Юность->Смерть;
Зрелость->Смерть;
}
</graph>
Если у вас узлы поименованы словосочетаниями, заключите их в кавычки, т. е.
<graph>
digraph G{
"Полет фантазии"->"Расход горючего";
}
</graph>
Поздравляем! Теперь вы способны рисовать графы в Wiki4Intranet. Остальной текст будет посвящен некоторым тонкостям использования Graphviz.
Внешний вид графа
«Dot» позволяет изменять внешний вид графа. Например, можно изменять форму фигур (прямоугольники, овалы, круги, параллелограммы, многоугольники), цвет и шрифт текста, цвет фона фигур, стиль стрелок и рамок фигур, подписи стрелок и т. д. Итак, основные объектами являются узлы («node») и ребра («edge»). Для того, чтобы настроить свойства всех узлов или ребер нужно вначале использовать команды
node[свойство1="значение1",свойство2="значение2",...] edge[свойство1="значение1",свойство2="значение2",...]
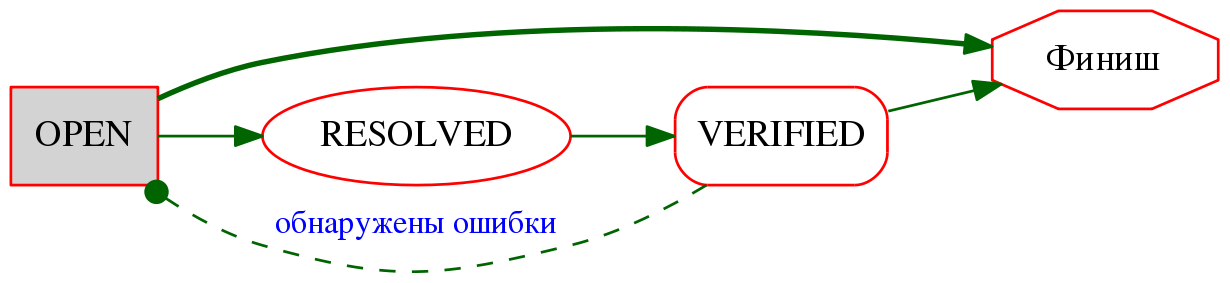
Также (в квадратных скобках после описания объекта) можно изменять настройки конкретного узла или ребра. Параметры графа, просто задаются в виде параметр=значение. Полезно запомнить параметр «rankdir», он может быть «TB» (top->bottom, параметр по умолчанию), или «LR» (left->right), и определяет, сверху-вниз, или справа-налево, нужно располагать узлы графа. Вот пестрый пример:
digraph G{
rankdir=LR;
node[color="red",fontsize=14];
edge[color="darkgreen",fontcolor="blue",fontsize=12];
OPEN[shape="rectangle",style="filled",fillcolor="lightgrey"];
CLOSED[shape="octagon",label="Финиш"];
VERIFIED[shape="rectangle",style="rounded"];
OPEN->RESOLVED->VERIFIED->CLOSED;
OPEN->CLOSED[style="bold"];
VERIFIED->OPEN[label="обнаружены ошибки",style="dashed",arrowhead="dot"];
}
на выходе будет
Если предполагается, что граф будут не только просматривать через IE, но и печатать, то необходимо установить ширину картинки, иначе при печати картинка будет обрезана. Для этого следует задать внутри описания
size="6.7,15";
Существенна только первая цифра. Число 6.7 подобрано эмпирически, оно обеспечивает печать полной картинки при настройках IE по умолчанию.
Уровни в графах
В «Dot» присутствует возможность связать узлы графа не только стрелками, но и уровнями отображения, что позволяет создавать шкалу и располагать узлы графа соответственно данной шкале. Для связывания используется следующая конструкция:
{ rank = same; "элемент уровня"; "элемент для привязки 1"; "элемент для привязки 2"; ..}
Например, при использовании следующей конструкции:
<graph>
digraph G{
node[fontsize=9];
{ /* шкала месяцев*/
node[shape=plaintext]; /* что бы не было видно рамок */
edge[color=white] /* что бы не было видно стрелок */
"март" -> "июнь" -> "сентябрь" -> "декабрь";
}
{ rank = same; "март"; "весна"; "a"; }
{ rank = same; "июнь"; "лето";}
{ rank = same; "сентябрь"; "осень"; "d"; }
{ rank = same; "декабрь"; "зима"; "e"}
"весна" -> "лето" -> "осень" -> "зима" -> "весна"
"a" -> "b" -> "c" -> "d" -> "e" ;
}
</graph>
на выходе получается:
Многосекционный узлы
Dot позволяет создавать многосекционные узлы при это каждая секция может быть поименована, и тогда ребра можно продоводить между секциями и узлами.
Для включения режима многосекционности устанавливается атрибут узла shape.
shape=record;
Секции описываются в атрибуте label узла, с помощью разделителя «|». Для именования секции ее имя указывается в <>. При описание ребра, исходящего или входящего в секцию, секция именуется следующим образом:
элемент:<имя_секции>
Например, из такого описания:
digraph structs {
rankdir=HR;
first [shape=record,label=" x1\n all | { x21 | <f0> x22| x23} | x3" ];
second [shape=record,label=" x22_1 | x22_2 | x22_3"];
first:<f0> -> second;
}
Получается следующее:
Гиперссылки на графах
Можно использовать атрибут «URL», задавая относительные или абсолютные гиперссылки для узлов и ребер. Например
<graph>
digraph G {
rankdir=LR;
SGML [URL="SGML"];
HTML [URL="HTML"];
XML [URL="XML"];
XHTML [URL="http://www.w3schools.com/xhtml/"];
SGML->HTML;
SGML->XML;
HTML->XHTML;
XML->XHTML;
SGML->XHTML[color="red",fontcolor="blue",label="ссылка на Google",URL="http://www.google.com"];
}
</graph>
Кластеры в графах
Программа «Dot» позволяет объединять узлы графов в кластеры для подчеркивания общности.
Кластер описывается следующим синтаксисом:
subgraph имя{
свойство1 = "значение1",свойство2="значение2",...
узел1;
узел2;
...
}
При этом имя подграфа должно начинаться с префикса cluster, иначе подграф не позволяет себя отобразить на экран(раскраска, контур, подпись, .. ).
Например:
digraph G {
rankdir=LR;
subgraph cluster0 {
node [style=filled,color=white];
style=filled;
color=lightgrey;
a0;
a1
label = "process #1";
}
subgraph cluster1 {
node [style=filled];
b0;
label = "process #2";
color=blue
}
start -> a0;
start -> b0;
a0 -> a1 -> end;
b0 -> end;
}
Цвета
Graphviz позволяет использовать широкую цветовую палитру, задавая цвета или по именам, в одной из известных палитр:
- Набор палитр Brewer-а, что удобно при автоматической генерации схем — задаваемые числовым индексом цвета в более-менее вменяемой палитре.
Кроме именованных цветов, можно использовать обычное трехбайтное шестнадцатиричное кодирование
color="#FF0EDD"
и выбирать цвета из палитры, например, на http://www.colorpicker.com/
Цвета и черно-белая печать
Graphviz позволяет использовать широкую цветовую палитру, однако, стоит не забывать, что контрастно выглядящие на цветном мониторе цвета, могут быть совершенно неразличимы после черно-белой печати. После проделанных экспериментов (Bug:11015), можно рекомендовать следующие палитры цветов (иллюстрированы на цвете ребер графа):

Формы вершин
Перечислим палитру возможных форм вершин (узлов).
Окончания ребер
Можно задавать стиль офомления начала («arrowtail») и конца («arrowhead») дуг (ребер):
![]() Чтобы работал arrowtail, для ребра нужно указать свойство dir=both или dir=back.
Чтобы работал arrowtail, для ребра нужно указать свойство dir=both или dir=back.
Неориентированные графы
Наряду с рисованием ориентированных графов, есть несколько методов для автоматического рисования неориентированных графов (будем рассматривать их на примере несложной ER-диаграммы).
В отличие от автоматического рисования направленных («directed») графов, основанных на ранговой модели, есть несколько подходов к раскладке ненаправленных графов.
Graph
Ненаправленный граф можно нарисовать с помощью рангового подхода (несмотря на ненаправленность ребер) — будет использоваться программа «dot». Как это будет выглядеть для простой ER-диаграммы, можно увидеть ниже.
Очевидна неоптимальность такого подхода для неориентированных графов.
Neato
Метод «neato» использует «энергетическую» (spring) модель, по сути, близкую к методу искуственного отжига — начиная с некоторого состояния вершины перемещаются, чтобы минимизировать некую потенциальную энергию. Рекомендуем для ненаправленных графов общего вида.
FDP
Метод «fdp» по сути, близок к методу «neato», и использует другую разновидность «энергетического» («spring») подхода. Также рекомендуется для ненаправленных графов общего типа.
Twopi
Метод «twopi» рисует графы с радиальной раскладкой. По сути одна вершина выбирается центральной, и помещается в центр, а остальные размещаются на последовательности концентрических орбит, вокруг этой вершины. Т.е. все вершины на расстоянии в «одно ребро» от центра, лежат на первой орбите, «в два ребра» — на второй и т. д.
CIRCO
Метод «circo» использует «circular layout». Выделяются двусвязные компоненты (каждая вершина имеет по крайней мере два ребра) и вершины этих компонент рисуются на некотором круге. «Дополнительные» ребра рисуются радиально и далее процесс повторяется. Пересечение ребер внутри круга минимизируется максимально возможным выносом ребер с круга за его периметр.
Версии для печати
Как известно, трудно добиться хорошего результата одновременно на экране и на принтере, в силу разных разрешений. Картинка экранного разрешения будет плохо (с «зазубринами») выглядеть на принтере, а картинка печатного разрешения, будет очень плохо выглядеть на экране (к сожалению, современные броузеры выполняют очень примитивный ресайзинг картинок при показе), и будет достаточно много «весить». Все соображения о печатных картинках также относятся к случаю, когда вы переносите (например, копируя вебстраницу из броузера через клипборд) содержимое MediaWiki-статьи в MS Word или другой текстовый редактор. Для такого, «печатного» случая (т. е. если у вас не примитивные графы, и вы собираетесь их печатать или переносить в другую систему верстки), мы сделали «печатную версию» всех перечисленных графов, с разрешением около 200 DPI. Для этого надо использовать те же самые тэги с постфиксом «-print», например «graph-print»,«neato-print», и т.п.:
Полученные картинки являются компромиссом, между весом, читаемостью на экране и читаемостью на бумаге. Желательно не использовать для совершенно тривиальных графов, или графов, которых вы не собираетесь печатать.
Ссылки и дополнительная документация
Онлайн-документация, +последние изменения, FAQ и прочее можно найти на домашней странице пакета http://www.graphviz.org/Documentation.php
Внимание! Данная статья выбрана для репликации во внешнюю базу знаний компании. Пожалуйста, не допускайте в этой статье публикацию конфиденциальной информации, ведения обсуждений в теле статьи, и более ответственно относитесь к качеству самой статьи — проверяйте орфографию, пишите по-русски, избегайте непроверенной вами информации.